 Here is an
image which illustrates these terms.
Here is an
image which illustrates these terms.Hamburg (Germany), the 3rd June 1997. Written by Nils Pipenbrinck aka Submissive/Cubic & $eeN
Ok, I guess it's now time to start working on the 3D section of my tutorial pages. 3D backface culling in object space is a topic which is easy to implement but can reduce some of the calculation costs. Backface culling is used in 3D rendering. It helps you to sort out those polygons in your scene database that won't be visible, since you want to remove them as fast as possible. Please note that in the age of pentiums and other fast processors the overhead of doing this stuff might be higher than the time you can save. I implemented it and found out that it's not really faster than normal backface culling. However, the results are much more accurate. One note before we start: Whenever I speak about tranformations I mean linear transformations. A tranformation may be built out of any number of the following actions, in any order or combination: Rotation, Scaling, Shearing (and if you work with 4x4 matrices, Translation).
We assume that all polygons are triangles, and that the vertices are ordered counter-clockwise. (If you're familiar with 3D graphics you'll know what I mean, otherwise you should first take a look at some other 3D tutorials.) Now just take a polygon, rotate it, scale it, do whatever you want to do with it and then project it into screen coordinates. We can now test if the polygon is visible using the screen coordinates: v1, v2, v3 are the points of the polygons in 2D space. (rotated and projected to 2D space)
now you calculate the two direction vectors that makes up the poly:
d1.x = v3.x - v1.x d1.y = v3.y - v1.y d2.x = v3.x - v2.x d2.y = v3.y - v2.y
If you now calculate the crossproduct of these two vectors you'll get another vector. This vector points out of the polygon (it's called the polygon normal vector if you don't already know this). If the z-component of this vector is negative the polygon faces away from the camera and the polygon can be skipped. Complete Formula: z = (d1.x * d2.y) - (d1.y * d2.x)
Normally about 50% of your polygons aren't facing the camera. That means that if you use this approach you would rotate and perspective-project 50% of the polygons without actually drawing them.
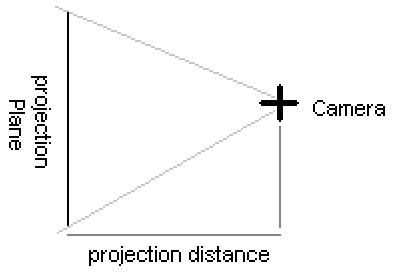
Before we start with the math we have to define some terms. The projection plane (your screen!) is located at the origin of the coordinate system, and your camera is located some distance behind this plane. The distance from the camera to the projection plane is called the projection distance.
 Here is an
image which illustrates these terms.
Here is an
image which illustrates these terms.
All the above calculations require that the object hasn't been
rotated or modified in any way. And this is the point of this culling
method: we can find out if a face is visible without touching the
polygons at all. First we need the position vector of the camera. If
you use the same definitions as I use the vector is CAM = <0,
0, -project_distance>
Now we reverse transform this vector into object space (that means,
if the object had eyes, where would it see the camera?). I'll discuss
how to do this below. Don't worry about it at the moment. The polygon
is visible if the following equation is true:
dotproduct(normal, CAM) >= cullpoint
where
normal is the normal vector of the polygon (in 3D).
CAM is the reverse transformed camera location vector.
cullpoint is dotproduct (normal, any vertix of poly).
Since the object must not be touched the normal can be calculated once before we start drawing and the cullpoint is a constant which won't change unless you modify the vertices or the normal (thus, compute it along with the normal vector). If your vertices move around or your object morphs you have to calculate the cullpoint and normal vectors every time you do the backface culling. In this special case you should rather use the 2D way because the normal vector calculation is very expensive. That's all. You need one simple 3D-dotproduct and one comparison to check if the polygon is facing you or not.
I already noted that you need to reverse transform the camera location vector CAM. If you have good knowledge of math you'll have no problems doing this. For all the others I'll give some comments on what I mean and how to do it. The backface culling MUST take the object transformation into account. One way to do this would be to transform the object vertices and normals and work with the camera location. This means that we still have to rotate all the vertices and normals before we know which polygons are visible and which are not. We still save the perspective projection unlike to the 2D approach, but the advantage of 3D culling is gone. The second approach would be to transform the CAM vector only. And this transformation is a little bit special. It must be the complete inversion of the object transformation. That means if you did the following with your object:
rotate x by 30 degree rotate y by 20 degree rotate z by 50 degree translate by <1,2,3>
you have to do the following with your camera vector:
translate by <-1,-2,-3> rotate z by -50 degree rotate y by -20 degree rotate x by -30 degree
You don't only have to reverse the sign of the transformation but also the ORDER in which you apply these transformations. I spent some days finding my error because I forgot to reverse the order of rotations! So be warned and don't make this mistake. If you organized your tranformations in a matrix you can simplify this a little bit: Just take your object transformation matrix, build the inverse and multiply it with the CAM vector. The inversion of a transformation matrix does exactly what you need: it reverses the meaning of a matrix. You can calculate the inverse matrix using the GAUSS-JORDAN algorithm or, if you're clever, you'll find a better way to calculate it. If your matrix is a combination of linear transformations (and I guess it will be unless you do very weird stuff) there are more efficient ways to do it. Hint: look into the books Graphic Gems and search for Angle- and Length-preserving matrices.
Many thanks go out to some folks who helped me to derive and implement this stuff. Those two who really helped me are Galvados (Orange) and John Carmack who was smart and friendly enough to help a frustrated 3D coder. Hasn't John proved that he has a good attitude answering my emails? I think he would be a good sceener! I'm not sure about all the 2D culling stuff. I typed it out of my mind and didn't test it. If you have any comments, notes or found any bugs please contact me. I'll continue writing tutorials as long as I get some feedback and know that writing this stuff isn't just wasted time. As always you might want to contact me.
© by submissive