
Hamburg (Germany), the 19th September 1999. Written by Nils Pipenbrinck aka Submissive/Cubic & $eeN
I learned a nice way to calculate bezier-curves a couple of weeks
ago. This algorithm is that nice and easy to understand. So if you
ever had problems remembering the basis-matrix of bezier curves don't
worry... after this article you'll never need it again.
First
remember what a bezier curve is:

It's a curve defined by 4 control-points (named a to d). The curve starts at the first point (a) and smoothly interpolates into the last one (d). The two points (b and c) in the middle define the incoming and outgoing tangents and indirectly the curvature of our bezier-curve.
I think the best way to explain the DeCasteljau algorithm is to use an example. The bezier-curve has 4 control-points. And we can connect these 4 points with 3 lines (shown in red). I also build 3 new points which are the midpoints of the new lines (shown as green dots).
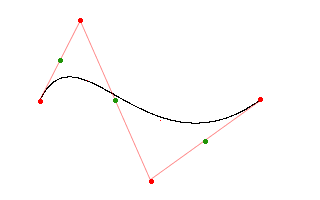
These points can again be used to build two new lines (green). Again we also calculate the midpoints of these lines (blue dots).
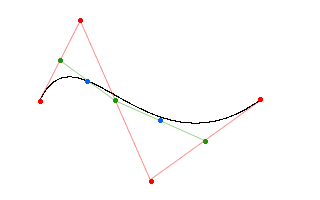
Finally we connect the blue dots and build a final line (blue. If you zoom into the image you might be able to see the blue line.. it's hard to see). Again we calculate the midpoint. This point is one of the points that define the bezier-curve.
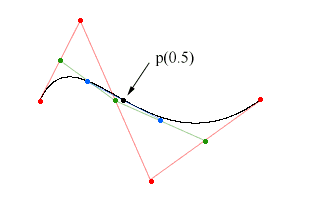
Now we can calculate one single point of the bezier curve. That's nice, but of no real use. Usually we want to calculate any point on the curve. To do this we only have to change the way we calculate the new points. Instead of always taking the midpoint we can use simple linear interpolation to calculate any point in the lines. If we do so we can calculate any point on the bezier-curve. And that's what we want to do.
I think there is not much to say about this simple C++ code. It's easy, and with the explanations above you should be able to understand how it works. Feel free to copy and modify this code...
#include <cstdio>
struct point
{
float x;
float y;
};
// simple linear interpolation between two points
void lerp(point& dest, const point& a, const point& b, const float t)
{
dest.x = a.x + (b.x-a.x)*t;
dest.y = a.y + (b.y-a.y)*t;
}
// evaluate a point on a bezier-curve. t goes from 0 to 1.0
void bezier(point &dest, const point& a, const point& b, const point& c, const point& d, const float t)
{
point ab,bc,cd,abbc,bccd;
lerp(ab, a,b,t); // point between a and b (green)
lerp(bc, b,c,t); // point between b and c (green)
lerp(cd, c,d,t); // point between c and d (green)
lerp(abbc, ab,bc,t); // point between ab and bc (blue)
lerp(bccd, bc,cd,t); // point between bc and cd (blue)
lerp(dest, abbc,bccd,t); // point on the bezier-curve (black)
}
// small test program.. just prints the points
int main()
{
// 4 points define the bezier-curve. These are the points used
// for the example-images on this page.
point a = { 40, 100 };
point b = { 80, 20 };
point c = { 150, 180 };
point d = { 260, 100 };
for (int i=0; i<1000; ++i)
{
point p;
float t = static_cast<float>(i)/999.0;
bezier(p,a,b,c,d,t);
printf("%f %f\n", p.x, p.y);
}
return 0;
}
One think I forgot.. This page here only dealt with cubic bezier curves. You can also calculate quadratic beziers (the ones defined with just 3 points). All you have to do is start with 3 instead of 4 points. The same can of course be done with more than 4 points. If you need a higher order bezier just use as many points as you want to... the algorithm works with any order beziers (I wonder who needs higher order curves...). As always you might want to contact me.
© by submissive